思想
一句话总结 Transfusion 的核心思想:
用一个统一的 Transformer,通过预测“下一个 token”,同时处理文本和图像的生成任务,把扩散模型的优势融入语言建模的训练范式。
1. 核心问题是什么?
-
当前的多模态模型通常对不同模态使用不同的训练方式:
- 文本 → 用语言模型(next-token prediction)
- 图像 → 用扩散模型(denoising training)
-
这导致:
- 模型结构复杂、训练成本高;
- 难以统一训练;
- 多模态共享参数受限。
Transfusion 提出的核心问题就是:
能否用统一的“next-token prediction”框架来训练一个模型,既能高质量生成文本,又能高质量生成图像?
2. 动机和设计 insight 是什么?
Insight #1:语言建模方式是简单且强大的
- Next-token prediction 已被 LLMs 验证为强泛化能力 + 超强扩展性的训练目标。
- 如果能用类似方式处理图像,也许能把图像生成和语言生成统一建模。
Insight #2:图像扩散的过程其实也可以“token 化”
- 传统扩散模型在 latent 空间里一步步去噪;
- 作者将这个过程 离散化(quantize) 成 token;
- 然后让 Transformer 一步步预测噪声残差 token,本质上就像语言模型预测下一个字。
Insight #3:训练方式的统一,带来架构的统一
- 模型只需要一个 decoder-only Transformer;
- 用一样的 loss(cross-entropy);
- 用一样的训练策略(next-token prediction);
- 实现统一结构 + 模态融合。
3. 方法结构简述
-
输入:
- 文本:用 subword tokenizer;
- 图像:先用 VAE 编码成 latent,再加噪声、离散化成 token;
-
模型:Decoder-only Transformer(GPT-style);
-
输出:
- 文本任务:预测下一个 subword;
- 图像任务:预测下一个噪声 token(= 学习如何去噪);
-
训练目标:统一的 cross-entropy loss,next-token 预测。
4. 实验和效果怎么样?
- 用统一方法训练了最大 70 亿参数的模型;
- 在文本任务上:表现接近纯 LLM;
- 在图像生成上:可比传统 diffusion(比离散 token-only 方法效果更好);
- 可以把图像压缩到非常低的 token 数量(如每图 16 个 patch)还保持质量。
5. 创新贡献总结(为什么它重要)
| 贡献点 | 意义 |
|---|---|
| 把扩散建模引入 token prediction 框架 | 解决模态统一问题 |
| 单模型同时胜任文本 & 图像生成 | 多模态能力强,推理统一 |
| 提出一种跨模态、从头训练、可扩展的训练范式 | 对未来的多模态基础模型启发巨大 |
| 简化结构:decoder-only transformer + 单一 loss | 更易训练、部署 |
总结金句
Transfusion 的本质是:用语言模型的方式去做图像扩散,从而统一多模态训练范式。
流程
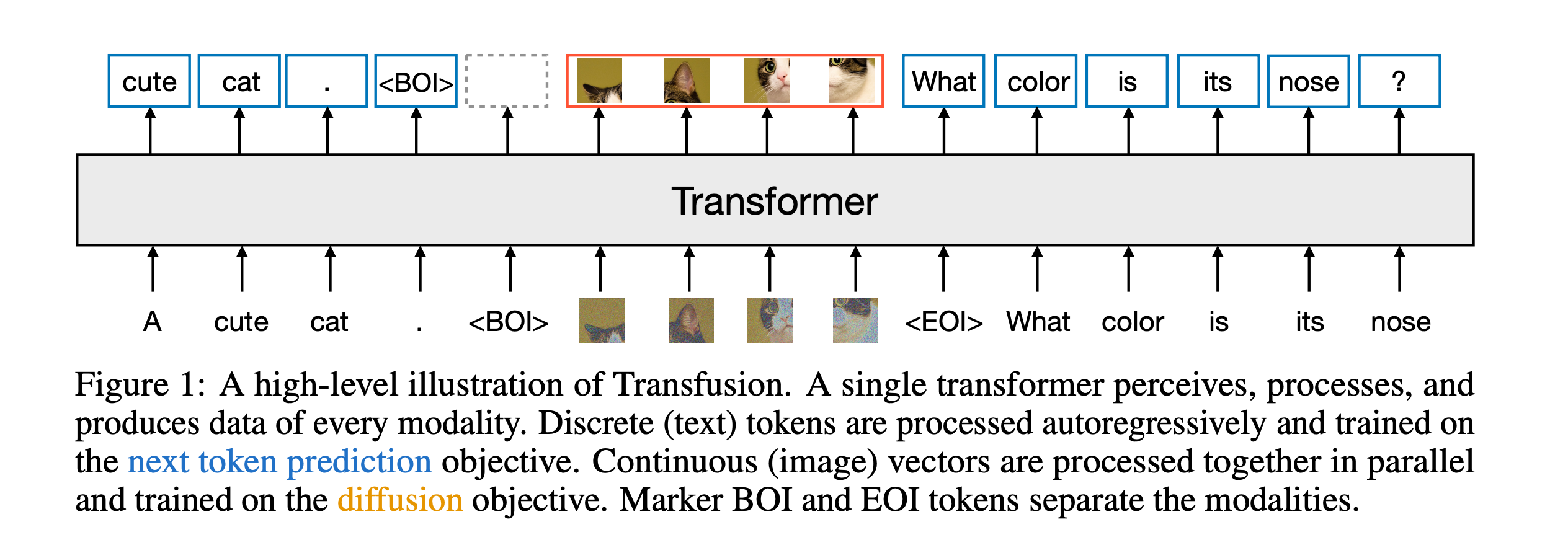
我们来详细聊聊《Transfusion》这篇论文中最核心的设计:如何用一个统一的 Transformer,通过预测下一个 token,同时处理文本和图像生成任务。
这件事的关键在于:统一 token 空间 + 统一预测方式(next-token prediction)+ 统一模型结构(decoder-only Transformer)。
核心目标:
设计一种方式,使得文本和图像都可以被表示成“token 序列”,然后用同一个 Transformer 来处理它们,就像 GPT 那样逐个预测下一个 token。
这个统一是怎么实现的?
我们拆成几个关键模块来看:
1. 文本部分:直接用语言模型的套路
- 文本输入 → 用常规的 subword tokenizer(如 BPE)编码成 token 序列;
- 模型任务 → 预测下一个 token;
- Loss → cross-entropy,和 GPT 一样。
没有新设计,就是普通语言建模。
2. 图像部分:借助 VAE + 离散化 + 扩散式 token
这是创新的关键!
2.1 图像编码
- 原始图像 → 输入到一个 VAE 编码器(可能是 Imagen/VQ-GAN 类似结构);
- 得到一个 latent 表示(比如 $z \in \mathbb{R}^{h \times w \times c}$);
- 这个 latent 更小、更精炼,后面只在 latent 空间操作。
2.2 加噪声(模拟扩散过程)
- 在 latent 上加噪声 $z_t = z + \epsilon$,模拟扩散模型中 t 步的 noisy latent;
- 这样就把扩散的“去噪问题”转化成“预测噪声”的任务。
2.3 离散化成 token
- 把 noisy latent 通过一个 codebook(比如 vector quantization)离散成 token;
- 这些 token 就是图像生成任务中要预测的目标;
- 换句话说,模型是在 noisy latent 的 token 序列上,预测残差噪声 token。
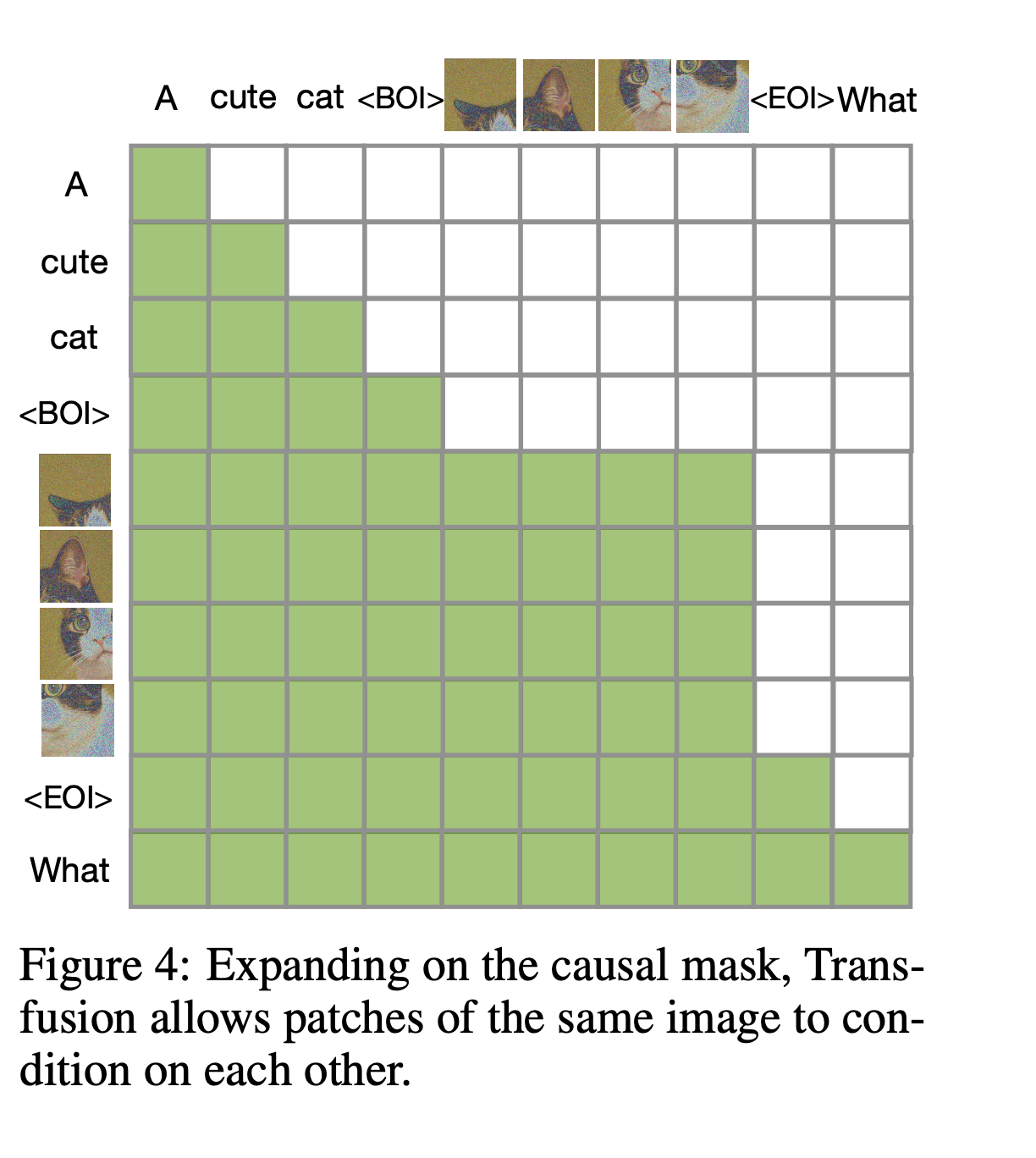
3. 模型结构:统一的 Decoder-only Transformer
无论输入是文本 token 还是图像 latent token,都拼成一个序列,送入 一个统一的 Transformer。
模型结构:
- Decoder-only(GPT-style):没有 encoder 模块,纯靠自回归;
- 模型中加了 模态 embedding(text/image) 和 time embedding(for diffusion steps) 作为条件;
- 所有任务共享参数,不区分分支。
模型输入举例:
[TEXT_TOKEN_1] [TEXT_TOKEN_2] ... [<EOT>] [IMG_TOKEN_1] [IMG_TOKEN_2] ...
4. 输出任务:统一用 next-token prediction
- 文本任务:预测下一个 subword;
- 图像任务:预测下一个 噪声 token(在 latent 空间中的 token);
- 所以整个模型都用 cross-entropy + next token loss 来训练。
总结一下:
作者通过 latent 表示 + 加噪 + 离散化为 token,把图像生成变成了一个“语言建模问题”,然后就能用语言模型的那一套(统一结构、统一 loss、统一训练)来处理图像。
推理阶段
目标:
我们希望使用 Transfusion 模型,从一个 prompt(可以是文本,也可以没有)开始,生成一张图像。
核心思想一句话:
Transfusion 把图像生成看作是 “一步步生成 latent token 序列”的过程,然后用 VAE decoder 把这些 token 转换成图像。
推理流程(Inference Pipeline)分成 4 步:
第 1 步:准备输入(Prompt)
- 你可以输入一段文本 prompt(例如:“A cat sitting on a sofa”);
- 也可以不给任何输入,随机生成;
- 文本会被编码成 token 序列,比如:
[T1, T2, ..., Tn, <EOT>] # 文本结束符
第 2 步:开始图像 token 的自回归生成
- 从
后,开始逐步生成图像的 token; - 每一个图像 token 对应于一个 “latent patch”(加噪的);
- 假设我们需要生成 32x32 = 1024 个 patch,那么就循环 1024 次,每次做:
P(t_i | t_1, ..., t_{i-1}) → 采样 → 得到 t_i
已有输入:[text tokens..., <EOT>]
输出 token: [134, 12, 199, ..., 48] # 共 1024 个
这些 token 是 VAE latent + 噪声 后再离散化得到的 token(等价于 latent 的编码索引),所以它们是“图像在 latent 空间的加噪 token 表示”。
第 3 步:token → latent(从 token 还原向量)
- 用 codebook / 词嵌入矩阵把 token 转成向量,每个 token 是一个 latent patch;
- 得到一个形状是 (32, 32, C) 的 latent tensor;
- 这就像是图像在 latent 空间的表示,但它是 noisy latent(不是纯净图像 latent);
第 4 步:VAE Decoder → 输出图像
- 把这个 latent 送入 VAE decoder;
- 得到最终生成图像:
latent → VAE decoder → 图像 ∈ ℝ^{256×256×3}
完整流程图(推理阶段)
[Prompt tokens] → Transformer → [图像 latent token sequence]
↓
codebook lookup / embedding projection
↓
得到 noisy latent (e.g. 32x32x4 tensor)
↓
VAE decoder
↓
输出图像
补充说明(关键点)
- 一步生成:不是像扩散模型那样走几十步,而是一步到位生成所有 latent token;
- ❗生成的是加噪 latent 的 token,而不是“干净图像的 token”;
- 不再做去噪,因为 decoder 直接学会了如何从 noisy latent 恢复出图像;
- 全程自回归生成,和 GPT 生成句子一样。
总结(关键认知):
| 问题 | 答案 |
|---|---|
| 最后生成的是什么? | 图像 latent 的 token(表示加噪 latent) |
| 是不是扩散模型那样多步生成? | ❌ 否,只生成一次 token 序列 |
| 最终图像怎么来的? | 用 VAE decoder 解码 token 还原出的 latent |
进一步问:
- 那这个 latent 是哪个时间步 t 的加噪版本?
- 这个 decoder 是怎么学会从 noisy latent 还原图像的?
- 可不可以生成干净 latent token 而不是 noisy 的?
问题 1:
这个 latent 是哪个时间步 t 的加噪版本?
答案:
Transfusion 固定选择一个时间步 t,通常是中间的某一值(如 t = 100),然后训练和推理都用这个时间步。
背后逻辑:
-
扩散模型是多步走 t = T → t = 0;
-
Transfusion 直接“跳过这些步骤”,只在某个固定 t 上加噪训练,让模型学会:
给定 noisy latent(对应 t),直接生成图像。
问题 2:
这个 decoder 是怎么学会从 noisy latent 还原图像的?
答案:
decoder(来自 VAE)在 VAE 预训练阶段就被训练为:可以从带噪 latent 中重建图像。
背后机制:
- VAE decoder 原本就是为了容忍 latent 空间中的扰动(noise)而设计的;
- 在 Transfusion 里,即使 latent 是有噪的,decoder 也能大致还原原始图像。
类比:
你可以把 decoder 想成“模糊图像的复原器”,它不是精确还原,而是:
从 noisy latent 中恢复出一个“自然的、高质量”的图像版本(可能不是原图,但像人拍的图)。
问题 3:
可不可以生成干净 latent token,而不是 noisy 的?
理论上可以,但
Transfusion 有意选择生成 noisy latent token
,原因如下:
为什么不生成干净 latent token?
- 建模难度高:干净 latent 分布复杂、不容易用自回归 token prediction 模型建模;
- 采样不稳定:没有加噪时的平滑性,更容易生成 artifact;
- 缺乏泛化性:小变化在 clean latent 上影响很大,不如 noisy 的鲁棒。
训练阶段
我们来一步步拆解 Transfusion 里图像是怎么变成 token 并训练的,并且用例子来帮你直观理解。这个过程一共分成三步:编码 → 加噪 → 离散化为 token,最终就可以像处理文本一样用 Transformer 来预测。
整体目标回顾
我们希望把图像变成 token 序列,然后像文本一样用 Transformer 来做 next-token prediction。
但图像是连续的,不能直接变成 token,所以我们得先 把图像处理成一组离散 token,这个过程包括:
- 用 VAE 编码图像;
- 在 latent 上加噪,模拟扩散;
- 把 noisy latent 离散化成 token。
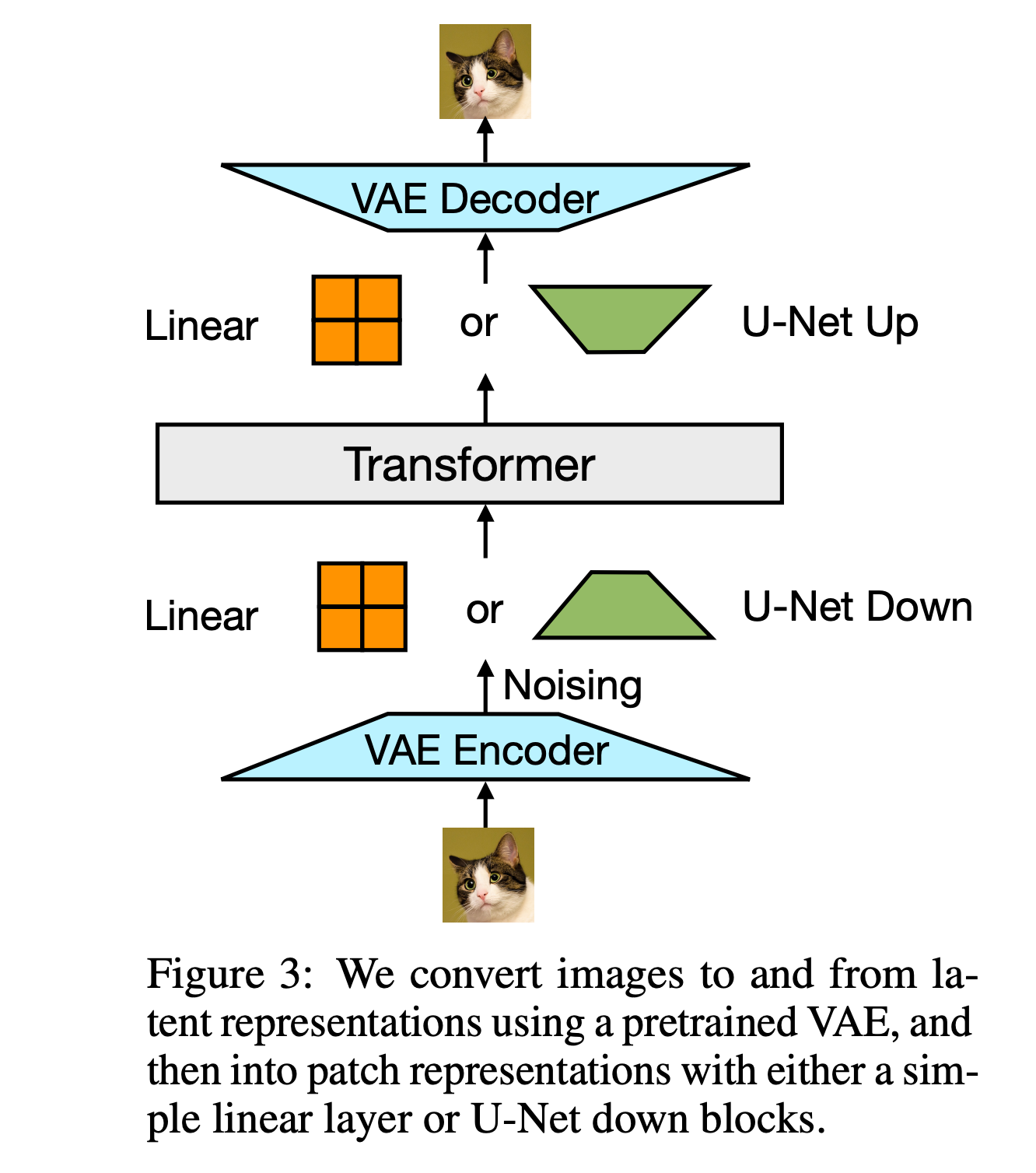
步骤 1:图像 → latent(用 VAE 编码)
目的:
把图像压缩成更小的“潜在表示”(latent),减少序列长度 & 表达信息。
怎么做:
-
输入图像 x \in \mathbb{R}^{256 \times 256 \times 3}
-
送入一个预训练的 VAE 编码器 E,得到 latent z = E(x) \in \mathbb{R}^{32 \times 32 \times 4}
- 也就是每张图被表示成 32×32 个 patch,每个 patch 是 4 维向量
举个例子:
一张图:
原图: 256x256x3
→ VAE 编码器 →
latent: 32x32x4
步骤 2:在 latent 上加噪声(模拟扩散)
目的:
像 diffusion 模型那样,在 latent 上逐步加噪声,形成一个“去噪预测”的任务。
做法:
- 在 latent 表示 z 上,加上高斯噪声 \epsilon \sim \mathcal{N}(0, I)
- 得到 noisy latent z_t = z + \sigma_t \cdot \epsilon
其中 \sigma_t 是控制噪声大小的参数,对应扩散的第 t 步。
举个例子:
假设 latent 里某个位置:
z = [0.2, 0.3, 0.1, -0.1]
ε = [-0.5, 0.7, 0.0, 0.2]
σ = 0.1
→ z_t = z + σ * ε = [0.15, 0.37, 0.1, -0.08]
这就是加噪后要预测的目标 latent。
步骤 3:将 noisy latent 离散化为 token
目的:
模型要预测“token”,不能处理连续向量 → 所以我们需要把 z_t 离散化成 token。
做法(两种思路):
- Vector Quantization(向量量化):
- 训练一个 codebook(类似于 VQ-VAE);
- 把每个 z_t[i,j] \in \mathbb{R}^4 匹配到 codebook 中最接近的向量 → 得到一个整数 token;
- 例如 z_t[i,j] 最近的是 codebook 的第 85 个向量 → token = 85。
- Linear Projection + Softmax(更简单):
- 把 z_t[i,j] 投影成一个 logits;
- 用 softmax 得到 token 的分布(和文本 token 一样)。
举个例子:
我们把图像编码成了 32x32 = 1024 个 latent 向量,加了噪声后,再量化成:
图像 token 序列 = [85, 112, 9, ..., 41] 共 1024 个 token
最后:模型训练方式
- 把这些 token 拼起来作为输入序列;
- 模型只需做一件事:预测下一个 token,就像语言模型一样;
- loss 也就是普通的 cross-entropy(像 GPT 一样);
- 模型不知道 token 是来自图像还是文本,只看 token + 模态 embedding。
小结流程图:
图像 →
→ VAE 编码 → latent z
→ 加噪声 → z_t
→ 离散化为 token → image_token_seq
→ 拼接序列 + next-token loss → Transformer
为什么选择生成 noisy latent token?
- 更像语言模型任务:
- 噪声让 latent 更接近正态分布,token 分布更规则;
- 更容易用 Transformer 做 next-token prediction。
- 受扩散模型启发:
- 扩散模型训练目标就是预测某个 noisy latent 的残差;
- 这里换成了 token → 用语言模型方法模拟 denoising。
- 训练和推理统一:
- 训练时学 noisy latent 的 token;
- 推理时生成同样形式的 token → 一致性好,稳定。